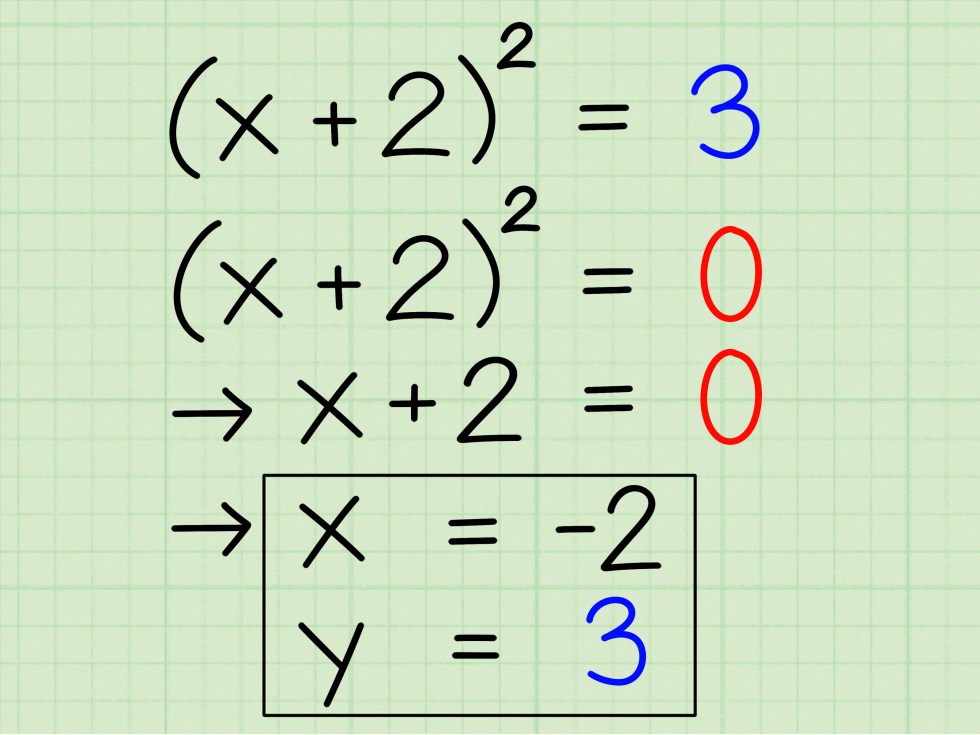Titik puncak suatu kuadrat atau parabola adalah titik tertinggi atau terendah dalam persamaan tersebut. Titik ini berada pada bidang simetri parabola. Segala sesuatu di sisi kiri parabola dengan sempurna mencerminkan segala sesuatu di sebelah kanan. Untuk mencari titik sudut suatu persamaan kuadrat, Anda dapat menggunakan rumus titik sudut atau melengkapi kuadratnya.
Gunakan rumus titik puncak
Tentukan nilai A, B, dan C. Dalam persamaan kuadrat, bagian x = a, bagian x = b, dan konstanta (bagian non-variabel) = c. Misalnya, Anda ingin menyelesaikan persamaan berikut: y = x + 9x + 18. Dalam contoh ini, a = 1, b = 9, c = 18.

Gunakan rumus titik sudut untuk mencari nilai x suatu titik. Titik sudutnya juga merupakan persamaan simetris. Rumus mencari nilai x pada kepala persamaan kuadrat adalah x = -b/2a. Untuk menemukan x, masukkan nilai yang diperlukan. Masukkan nilai A dan B. Tuliskan cara kerjanya.
x=-b/2a
x=-(9)/(2)(1)
x=-9/2

Mensubstitusikan nilai x ke dalam persamaan awal akan menghasilkan nilai y. Jika sudah mengetahui nilai x, substitusikan ke persamaan awal nilai y. Anda dapat memikirkan rumus untuk mencari titik sudut persamaan kuadrat sebagai (x, y) = [(-b/2a), f(-b/2a)] . Artinya untuk mencari nilai y, Anda perlu menggunakan rumus mencari nilai x dan memasukkannya kembali ke dalam persamaan. Berikut cara melakukannya:
kamu = x + 9x + 18
kamu = (-9/2) + 9(-9/2) +18
kamu = 81/4 -81/2 + 18
kamu = 81/4 -162/4 + 72/4
kamu = (81 – 162 + 72)/4
r = -9/4

Tulis nilai x dan y sebagai pasangan terurut. Jika Anda sudah mengetahui x = -9/2 dan y = -9/4, tulislah sebagai pasangan terurut (-9/2, -9/4). Titik sudut persamaan kuadrat adalah (-9/2, -9/4). Jika kita membuat grafik parabola ini, maka titik tersebut akan menjadi titik terendah/minimum parabola karena x positif.
Lengkapi perseginya

Tulis persamaannya. Kuadrat sempurna adalah cara lain untuk mencari titik sudut persamaan kuadrat. Jika Anda menggunakan cara ini dan menyelesaikannya sampai akhir, Anda bisa langsung mendapatkan koordinat x dan y tanpa harus memasukkan koordinat x pada persamaan awal. Jika ingin menyelesaikan persamaan kuadrat berikut: x + 4x + 1 = 0.

Bagilah setiap bagian dengan faktor x. Dalam hal ini, parameter x adalah 1, jadi Anda dapat melewati langkah ini. Membagi setiap bagian dengan 1 tidak ada bedanya.

Pindahkan bagian konstan ke ruas kanan persamaan. Konstanta adalah bagian yang tidak mempunyai koefisien. Dalam soal ini, konstanta adalah 1 . Pindahkan 1 ke sisi lain persamaan dengan mengurangkan 1 di kedua sisi. Berikut cara melakukannya:
x + 4x + 1 = 0
x + 4x + 1 -1 = 0 – 1
x + 4x = – 1

Lengkapi kotak di sebelah kiri persamaan. Caranya, cari (b/2) dan tambahkan hasilnya pada kedua ruas persamaan. Karena 4x adalah bagian b dari persamaan ini, kita masukkan 4 untuk b .
(4/2) = 2 = 4. Sekarang tambahkan 4 pada kedua ruas persamaan untuk mendapatkan:
x + 4x + 4 = -1 + 4
x + 4x + 4 = 3

Faktorkan ruas kiri persamaan. Kita dapat melihat bahwa x + 4x + 4 adalah kuadrat sempurna. Persamaan ini dapat ditulis dalam bentuk (x + 2) = 3.

Gunakan gambar ini untuk mencari koordinat x dan y. Anda dapat mencari koordinat x dengan menyetel (x + 2) ke 0. Berapakah nilai x jika (x + 2) = 0? Jika offsetnya +2 maka variabel x harus -2, jadi koordinat x -2. Koordinat y adalah konstanta di sisi lain persamaan. Jadi y = 3. Anda juga dapat mempersingkatnya dan mengganti tanda angka dalam tanda kurung untuk mendapatkan koordinat x. Jadi titik puncak persamaannya adalah x + 4x + 1 = (-2, -3).